Potência Média de uma Força
Vimos que o trabalho W de uma força F corresponde à energia acrescentada (ou retirada) de um corpo enquanto o mesmo se desloca sob ação dela.
Esse trabalho acontece em um certo intervalo de tempo Δt.
A razão entre o trabalho W realizado e o intervalo de tempo Δt é chamada de potência média (Pm) da força. Ela representa a quantidade média de energia transferida (ou retirada) do corpo a cada unidade de tempo.
Se a força F for constante, ela irá transferir (ou retirar) sempre a mesma quantidade de energia do corpo a cada unidade de tempo. Então chamamos apenas de potência (P) da força.
No sistema internacional de unidade (S.I.), a unidade de potência é o watt (W), que é equivalente ao Joule/segundo (W=J/s).
Então, se conhecemos a potência média Pm (ou a potência P) de uma força e o intervalo de tempo Δt em que realizou certo trabalho W, podemos determiná-lo da seguinte forma:
Exemplo 1
Um guindaste suspende uma carga com massa M = 5000kg a uma altura de 20m, em 1,0 minuto. A potência do guindaste é constante e igual P=25kW.
Considere g=10m/s².
a) Qual o trabalho realizado pelo guindaste para elevar esta carga?
b) Qual o trabalho do peso P da carga nessa suspensão?
Resolução:
a)
P=25kW=25000W
Δt=1,0min = 60s Assim:
b) O peso P da carga tem direção oposta ao deslocamento d (para cima). Vamos considerar que vetores para cima são negativos, assim:
Cuidado! Agora P representa o peso da carga.
Como o peso P é oposto ao deslocamento d (para cima), vamos considerar que o vetor d tem sentido para cima e é negativo (d=-20m). Assim:
Isso significa que enquanto o guindaste dá energia cinética à carga (1,5MJ), a força peso lhe tira energia cinética (-1,0MJ).
Mas a carga está no campo gravitacional da Terra. Ao ao ser elevada a uma altura de 20m passa a ter energia potencial gravitacional "armazenada". O campo gravitacional é análogo a uma "mola" invisível que é esticada e armazena energia.
A energia cinética que a força peso retira na subida ao realizar trabalho (-1,0MJ) se converte em energia potencial gravitacional (1,0MJ).
A energia mecânica da carga só varia mesmo devido à ação da força feita pelo guindaste, que lhe dá energia cinética ao realizar trabalho.
Gráfico Potência x Tempo
Considere o gráfico abaixo que representa a potência P em função do tempo t, referente a uma força constante que tem a mesma direção do deslocamento:
A área entre a linha do gráfico e o eixo do tempo representa o trabalho W realizado pela força que tem potência P₀ no intervalo de tempo Δt.
Mas este resultado serve também para gráficos em que a potência P varie com o tempo. Destacando, que áreas acima do eixo do tempo representam trabalhos positivos, e abaixo do eixo do tempo, trabalhos negativos.
Exemplo 2
O gráfico abaixo representa a potência P em função do tempo t, referente a uma força que tem a mesma direção do deslocamento.
Qual o trabalho da força entre 0 e 20s?
Resolução:
A área A₁ (triângulo) corresponde ao trabalho positivo W₁, enquanto a área A₂ (trapézio), ao trabalho negativo W₂. Assim:
Resposta: O trabalho entre 0 e 20s é W=25J.
Potência Média e Velocidade Média
Vimos que:
Mas:
Assim:
Se a força F e a velocidade v são constantes e têm a mesma direção e sentido, teremos:
Logo, a potência P também é constante.
Exemplo 3
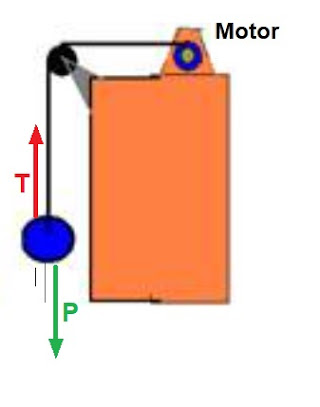
Um motor de potência igual a 270W, funcionando como elevador, eleva um corpo a 10m de altura, com velocidade constante v=3,0m/s.
Qual a tração T no fio?
Resolução:
Para que o corpo seja erguido com velocidade constante, significa que o módulo da tração T no fio (que o puxa para cima) deve ser igual ao módulo do peso P do corpo, para que a força resultante seja nula FR=0, e consequentemente também a aceleração a=0.
Se conhecêssemos a massa m do corpo poderíamos determinar seu peso P, logo também valor de T, mas não conhecemos.
No entanto, vimo que a potencia P da tração é a mesma do motor. Assim:
Cuidado! Em algumas equações P representa o peso, em outras, a potência de uma força.
Resposta: A tração tem módulo de 90N.
Verifique que o trabalho da tração (positivo) tem o mesmo módulo do trabalho do peso (negativo), já que estas forças têm o mesmo módulo.
Rendimento de um Motor
A potência total Pt de um motor nunca é usada completamente para realizar o trabalho que é desejado. Parte dessa potência total (energia liberada por unidade de tempo) é dissipada e é perdida, transformando-se em calor, ruído.
A parte da potência total que sobra para realizar o trabalho desejado é chamada de potência útil Pu.
O rendimento h de um motor é a razão entre a sua potência útil e a total:
O rendimento de um motor representa a sua capacidade de realizar trabalho útil (Wu).
Essa razão nos dará sempre um número entre 0 e 1, por exemplo, h = 0,3, mas sempre é representado em forma percentual, h = 0,3 = 30%.
Uma outra forma de calcular o rendimento, é:
Onde Et é a energia total que o motor utiliza para funcionar naquele intervalo de tempo. Essa energia pode ser elétrica, química (combustível por exemplo).
Exemplo 4
Um automóvel de massa 800kg partiu do repouso em uma estrada retilínea e horizontal, devido à ação de uma força constante de 1800N, paralela à estrada e aplicada por seu motor que tem rendimento de 45%. Ao percorrer 400m, sob a ação exclusiva dessa força, o consumo de energia proveniente do combustível foi, no mínimo, igual a:
a)6,4MJ
b)4,8MJ
c)3,2MJ
d)2,0MJ
e)1,6MJ
Resolução:
Um motor com rendimento de h = 45% é o mesmo que de h =0,45.
O trabalho útil Wu realizado pelo motor foi fazer com que força F=1800N feita por ele deslocasse o automóvel por uma distância d=400m:
Resposta: O motor precisará de 1,6MJ de energia proveniente do combustível para realizar o trabalho útil de deslocar o automóvel 400m.
Agora vamos testar o que aprendemos?
No link abaixo você poderá acessar uma lista de exercícios sobre o que estudamos até aqui.
É possível ver a resposta correta de cada questão, bem como a respectiva resolução.
Mas primeiro você deve tentar fazer sozinho no seu caderno, e só depois ver a resposta ou comparar com a resolução, ok?!
9